
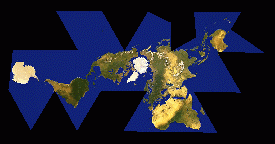
 Basically, Fuller started with the data for the spherical Earth surface. He
projected the data from the sphere onto an icosahedron -- the twenty- sided
Platonic solid -- and then unfolded that icosahedron out flat.
Basically, Fuller started with the data for the spherical Earth surface. He
projected the data from the sphere onto an icosahedron -- the twenty- sided
Platonic solid -- and then unfolded that icosahedron out flat. 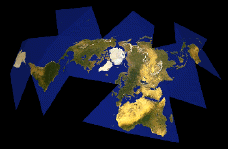 My animation of
an unfolding Dymaxion Map is available as a 1.4 meg ZIPped
640x480 QuickTime or as a 40k ZIPped 320x240 QuickTime
or as a 400k
160x120 Java animation.
My animation of
an unfolding Dymaxion Map is available as a 1.4 meg ZIPped
640x480 QuickTime or as a 40k ZIPped 320x240 QuickTime
or as a 400k
160x120 Java animation. 
 Basically, Fuller started with the data for the spherical Earth surface. He
projected the data from the sphere onto an icosahedron -- the twenty- sided
Platonic solid -- and then unfolded that icosahedron out flat.
Basically, Fuller started with the data for the spherical Earth surface. He
projected the data from the sphere onto an icosahedron -- the twenty- sided
Platonic solid -- and then unfolded that icosahedron out flat.
The advantages of this method are many: for one thing, it's possible to align the surface data with the icosahedron in such a way that, when unfolded, no landmass is cut into, which allows us to see the Earth's landmasses as one continent (this is where my illustration falls short; note that the landmass is cut into in a couple of spots); also, this method results in nearly no distortion of either size or shape of the landmasses, unlike most other projections (the familiar classroom Mercator map or the Peters projection, for example).
Anyway, this illustration was made using a C program to output Persistence of Vision Raytracer files, which were then raytraced on a DEC Alpha running OSF/1. Each of the 78 frames took about four minutes at 640x480 antialiased. The resulting Targa files were then nailed together into a QuickTime movie using movieconvert on an SGI Indy.
The mapping was done in POV by spherically mapping what looks like a GeoSphere graphic of the Earth around the sphere or icosahedron. That's where the mathematical inaccuracy comes in.
Both animations are hereby released to the public domain.
Thanks to the following information sources:
And, of course, thanks to the works of Bucky Fuller.
|
Chris Rywalt crywalt@westnet.com Copyleft © 1995 Christopher Rywalt. |